- parametric Bayesian filter
- algorithm for estimating the values of measured variables over time, given continuous measurements of those variables and the amount of uncertainty in those measurements
- estimate using past (possibly noisy) observations and present (and possibly noisy) observations
Assumptions
- noisy sensor
- noise can be modelled using Gaussian Distribution PDF
- initial prior knowledge (state) is also a Gaussian Distribution PDF
Algorithm
1. Predict Step
predict the current state given the previous state and the time that has passed since
- state
- prediction variable gaussian distribution
- mean vector (of the prediction variable) and
- covariance of prediction variables (uncertainity or noise in prediction variables)
- e.g. mean and covariance of position and velocity of an object
- prediction variable gaussian distribution
- state-transition matrix (F): relates the previous state to the current one
- prediction equations
- μp = F μt
- μp = predicted mean vector
- μt = mean vector at t
- predicted covariance matrix
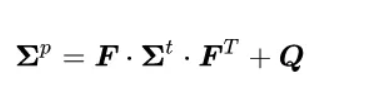
- Q: process noise
- encapsulates uncertainty created by the time that has passed since we last updated the state,
- μp = F μt
2. Update Step
- combine the predicted state with an incoming measurement
- input two possible states and outputs a new state
- Bayesian inference
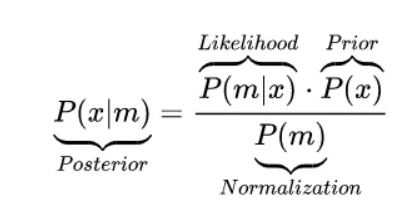
- x = actual position
- m = measured position
- prior: predicted state
- prior and likelihood are assumed to be Gaussian Distributions
- Normalization i.e measurement probability distribution → empirically calculated
- Posterior probability (updated state) calculated is also a Gaussian Distribution

- H → linear transformation that takes us from the state space to the measured space
- Kalman gain
- factor by which we incorporate the new sensor information into the updated state
- Errorestimate / (Errorestimate + Errormeasured )
- ( 0, 1)
- 0 → estimate error =0 → estimate is perfect
- 1 → measure error =0 → measure is perfect, estimate is imperfect
1-D case
- object tracking in 1-dimension
- assume constant velocity in 1-dimension
- let state = x, v → position, velocity
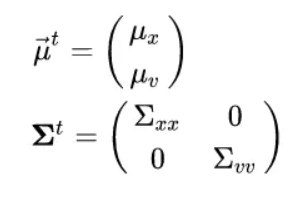
- initially there is no covariance between the velocity and position.
- Predict step equations
- mean vector prediction
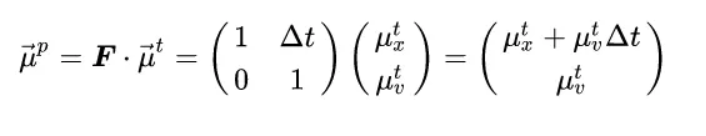
- F picked based on constant velocity assumption
- Solving for covariance
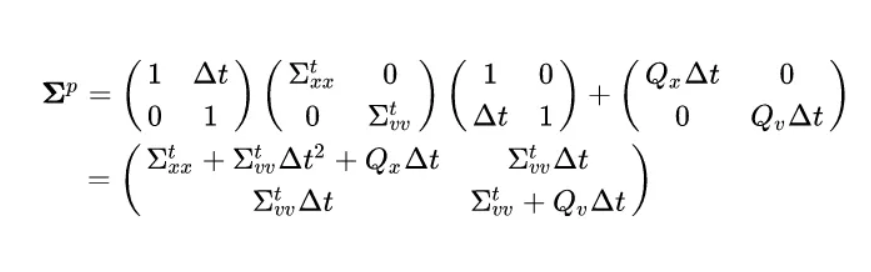
- introduces off-diagonal elements in the covariance matrix
- Update Step equations
Pros
- updates are simple and efficient
Cons
- unimodal distribution
- class of motions restricted by linear model