Reinforcement Learning

• learning to make decisions from sequential interactions
• Reinforcement Learning (RL) allows us to take the appropriate action at each stage of a sequential decision making problem in order to maximize some utility eventually

Objective

1. Find solutions
   • e.g. A program that plays chess really well
2. Adapt online, deal with unforeseen circumstances
   • e.g. A robot that can learn to navigate unknown terrains
   • i.e. objective is not just about generalization — it is also about continuing to learn efficiently online, during operation

The Reward Hypothesis

Any goal can be formalized as the outcome of maximizing a cumulative reward

See Intelligence

• RL Agent:

  Intelligent Agent

  an agent acting in an intelligent manner. It perceives its environment through observations, takes actions autonomously in order to achieve goals, and may improve its performance with learning or acquiring knowledge.

  Link to original

• agent state: internal state of the agent
• environment:

  Environment

  world in which the agent operates

  Environment State

  complete description of the state of the environment

  Observation

  partial description of the state of the environment

  Full Observability

  Observation = Environment state

  Link to original

The interaction loop

At each timestep t

1. the agent:
   • Receives observation O_t (and reward R_t )
   • Executes action A_t
2. The environment:
   • Receives action A_t
   • Emits observation O_t+1 (and reward R_t+1)

Action Space

• set of all possible actions in an environment
• could be discrete or continuous space

Reward

• The reward R_t is a scalar feedback signal from the observation
• The reward can be coming from the environment or part of the agent
• since the reward can be negative, we can see it as a penalty as well. In this case, the agent might need to minimize the penalty at every timestep. Thus, the above setup illustrates how the system is flexible enough to force the agent to take the best sequence of actions as fast as possible.

Cumulative Reward

• The agent wants to maximize the cumulative reward or return G
• G_t = R_t+1 + R_t+2 + R_t+3 …
• Recursively, we can write
  • G_t = R_t+1 + G_t+1
• Note these are cumulative future rewards

Discount Factor

• trades off importance of immediate vs long-term rewards
• rewards that come sooner are more likely to happen since they are more predictable than the long-term future reward.
• G_t = R_t+1 + γR_t+2 + γ²R_t+3 …
  • γ ∈ [0,1]
• G_t = R_t+1 + γG_t+1
• 
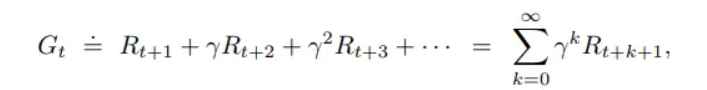
• if γ = 0, only near term rewards (myopic)
• if γ = 1, then all rewards are equally important, and the order of rewards are not important
• γ usually between 0.95 and 0.99

Tasks

• A task is an instance of a RL problem
• 2 types
  • Episodic task:  starting point and an ending point (a terminal state)
  • Continuing task:  continue forever (no terminal state)

Value

• The value v is the expected cumulative reward from being in an agent state s
• v(s) = E [ G_t | S_t = s ]
• value depends on the actions the agent takes + state
• agent’s goal is to maximize value by picking suitable actions
• Recursively, we can write
  • v(s) = E [R_t+1 + v(S_t+1) | S_t = s]
• Goal : Select actions to maximize the value
• Actions may have long term consequences and this value function takes that into consideration
  • It may be better to sacrifice immediate reward to gain more long-term reward

Action Values

• another way of defining values on the actions instead of states
• The action value q is the expected cumulative reward from being in a state s and then taking an action a
• q(s,a) = E [ G_t | S_t = s, A_t = a ]

Rewards and values define utility of states and action, and there is no supervised feedback. Instead, there is only the reward value (higher the better)

Agent

• Components
  • agent state
  • policy
  • value function estimates (optional)
  • environment model (optional)
• all components are functions, and so can be modelled using Neural Networks
  • see Deep Reinforcement Learning
  • some assumptions are often violated, like IID

Agent State

• internal state, everything that the agent takes along from one timestep to the next
• The history is the sequence of observations, actions and rewards that the agent experiences
  • H(t) = O₀, A₀, R₁ … O_t-1, A_t-1, R_t, O_t
• The history is used to construct the agent state S_t
• Markov Decision Processes (MDPs)
  • A decision process is Markovian if
    • the probability of a reward and subsequent state doesn’t change if we add more history
    • p(R, S_t+1 | S_t, A_t) = p(R, S _t+1 | H_t, A_t )
    • the agent state contains all we need to know from the history
      • once the state is known, history may be discarded
      • The full environment + agent state is Markovian
        • because it contains everything in history
        • but too large to be contained in agent state typically
      • the full history that the agent experiences is also Markovian
        • but again too large, and growing to be contained in agent state
      • typically, the agent state is some compression/function of the history
• S_t+1 = u(S_t, A_t, R_t+1, O_t+1)
  • u → state update function, compression function
  • could be simply a concatenation of A, R and O, in which case its is simply the history H, but that is too large
  • constructing a full Markovian agent state is often not feasible
    • use some approximation

• Markov Property

  the effects of an action taken in a state depend only on that state and not on the prior history

  Link to original

Policy

• An action selection policy
• defines agent’s behaviour
• A mapping from states to actions.
  • π : S → A (or probabilities over A)
•  Deterministic Policy
  • A = π(S)
• Stochastic Policy
  • a probability distribution over states and actions
  • π(A|S) = p (A|S)

Value Function Estimates

value function can be written as

• v_π(s) = E [ G_t | S_t = s, π ]
  • value function is dependent on the policy that picks actions given states
  • ⇒ v_π(s) = E [ R_t+1 + γR_t+2 + γ²R_t+3 … | S_t = s, π ]
  • ⇒ v_π(s) = E [ R_t+1 + γG_t+1 | S_t = s, A_t ~ π (s)]
  • ⇒ v_π(s) = E [ R_t+1 + γv_π(s) | S_t = s, A_t ~ π (s)]
• use v_π to
  • evaluate desirability of states
  • evaluate policies
  • come up with new policies
• value of a state is the expected discounted return the agent can get if it starts in that state, and then acts according to the chosen policy.
  • if no explicit policy, then the policy is to choose the state with the max value

Bellman Equation

• highest possible value v(s) = max E [ R_t+1 + γv(S_t+1) | S_t = s, A_t = a ]
  • does not depend on the policy

Environment Model

• predicts what the environment will do next
• P might predict the next state
  • P(s, a, s’) ~ p(S_t+1 = s’ | S_t = s, A_t = a)
• R might predict the next reward
  • R(s,a) ~ E[ R_t+1| S_t = s, A_t = a]
• models can be probability distributions or expectations

Types of RL

• Value based
  • no explicit policy
  • policy = value function
  • Algorithms
    • Q-Learning
    • Deep Q-Learning
• Policy based
  • no explicit value function
• Actor-critic
  • both policy and value functions
  • actor
    • policy
  • critic
    • critics the policy
    • value function used to update the policy
• Model-free
  • may have policy/value function
  • no explicit environment model
• Model based
  • optionally policy/value functions
  • have an environment model

Sub problems

• Prediction and Control
  • Prediction
    • predicting/evaluating the future for a given policy
  • Control
    • optimizing the future, i.e. finding the best policy
• Learning and Planning
  • Learning
    • environment initially unknown, agent learns by interacting
    • absorbing new experiences from the interaction loop
  • Planning
    • an environment model is given or learnt
    • agent plans in the model to optimize the policy
    • environment model might be inaccurate
      • policy might not be the best policy in the real world
    • any additional internal computational process, without looking at new experiences
• Exploration-Exploitation Tradeoff