see probability
Bayes’ theorem is expressed as:
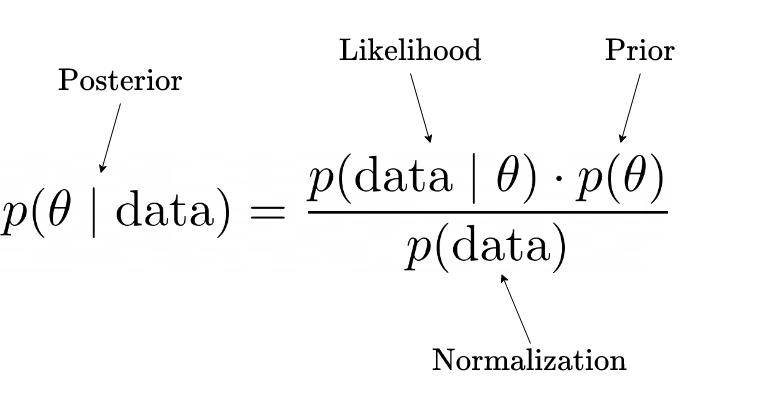
- P(X∣θ) is the likelihood, the probability of the data X given the parameters θ.
- probability distribution of the observed evidence given a parameter value
- P(θ) is the prior distribution, our initial beliefs about the parameters.
- a.k.a. prior belief,
- probability distribution of the parameters before evidence is taken into account
- P(X) is the marginal likelihood or evidence, which is the probability of the data under all possible parameter values
- normalization term
- P(X)=∫P(X∣θ)P(θ)dθ
- probability distribution of observed evidence independent of parameters
- P(θ∣X) is the posterior distribution, the probability of the parameters θ given the data X.
- provides a complete description of our updated beliefs about the parameters after observing the data