Object Tracking

• More than just Object Detection
• estimate the object position, but also incorporate the position predicted by dynamics
  • expectation of the object’s motion pattern

Challenges

• loss of 3D in 2D projection
• unusual poses
• occlusion , self occlusion

Simplifying the problem

• distinct a-priori colours (skin colour)
• multiple cameras
• prior knowledge - number of objects, object types, background

Tracking with Dynamics

Assumptions

• continuous motion patterns
  • camera, gradual change/smooth trajectory

Dynamic Inference Model

• x → estimated positions, y→ measured positions/ observations
• P(X_t | X_t-1) and P(Y_t | X_t) are assumed to be some known distributions
  • Gaussian Distribution is commonly used
• Goal: Estimate P(X_t | Y₁ … Y_t)
• at any point t we have P(X_t-1 | Y₁ … Y_t-1)
• 
• 
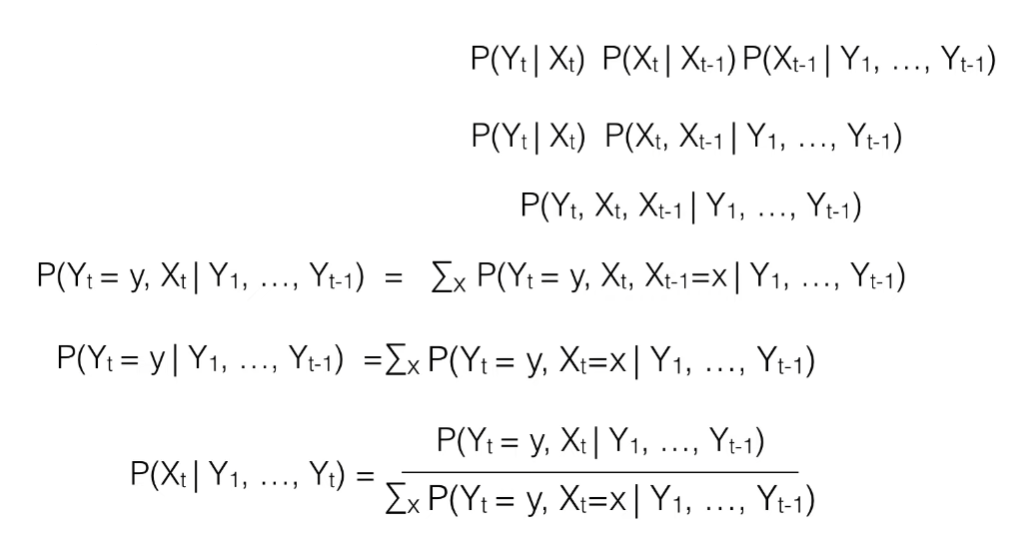
  • can be used instead to reduce computation cost

Algorithms

• Kalman Filter - parametric Bayesian filter
• Particle Filter - Non parametric Bayesian filter

Tracking by detection

• fixed camera scenarios
• limited background motion scenarios

Using Gaussian Mixture Models

see Gaussian Mixture Models

• For each pixel
  • compute pixel color histogram H using first N frames
  • Normalize histogram H = H / ||H||
  • Model H as a mixture of 3-5 gaussians
  • for each subsequent frame
    • pixel value X belongs to gaussian k for which
      • ||X - μ_k|| is min and
      • ||X - μ_k|| < 2.5σ_k
    • pixels are background most of the time. So gaussians with large evidence/scale ω and small σ are background. if ω/σ is large classify as background else foreground

tip for optimizing: instead of fitting gaussians in every frame, check if the new image intensity histogram and the old one differs by a lot, if yes then fit gaussians else skip