Camera Calibration

Method to find a camera’s internal and external parameters

Linear Camera Model - Forward Imaging Model

• mapping from 3D → 2D
• world coordinate frame (3D) → coordinate transformation to camera coordinate frame (3D) → perspective projection to image coordinates in the image frame (2D)
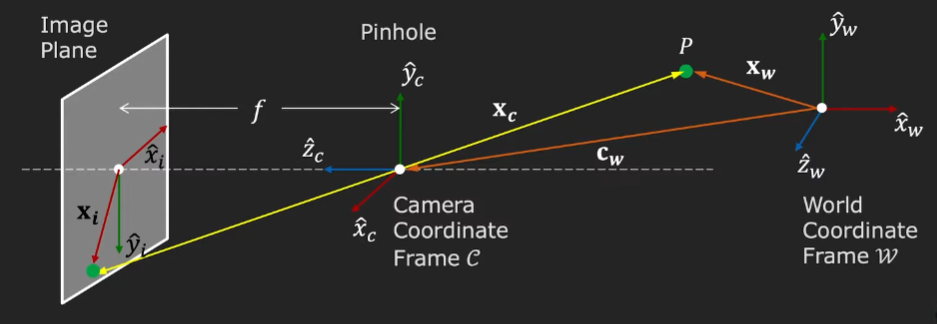
• World-to-camera transformation
  • camera extrinsic parameters =
    • rotation matrix
    • translation vector
  • combine to form an extrinsic matrix
• Perspective Projection Equations
  • from camera coordinate to image plane
  • 
  • where u,v are the positions in the image, x_c ,y_c, z_c are positions in camera coordinate frame
  • camera intrinsic parameters =
    • f is the effective focal length
    • o is the principal point
  • the equations are transformed into linear equations using homogenous coordinates resulting in an intrinsic matrix
• Projection matrix
  • can combine extrinsic and intrinsic matrix into a single projection matrix
  • using some image of a known real-world size of an object, it is possible to calculate this projection matrix
  • the projection matrix can also be decomposed back into the extrinsic and intrinsic matrix