the degree of agreement among independent observers who rate, code, or assess the same phenomenon.
Cohen’s Kappa
takes into account the possibility of the agreement occurring by chance
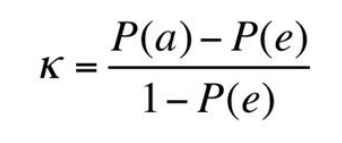
- P(a) = observed agreement, proportion of times judges agreed
- P(e) = expected agreement, proportion of times judges expected to agree by chance
Example
For 2 annotators and a binary classification problem,
- P(a) = P(A1=yes, A2=yes) + P(A1=no, A2=no)
- P(e) = P(A1=yes) * P(A2=yes) + P(A1=no) * P(A2=no)
Interpretation
unacceptable < 0.6 < substantial/tentative conclusions < 0.8 < definite conclusions
Scott’s Pi
improve on simple observed agreement by factoring in the extent of agreement that might be expected by chance
Fleiss’ kappa
Scott’s pi extended to more than two annotators